Histograms and Density Plots in Python

Analysis of Single Continuous Variable

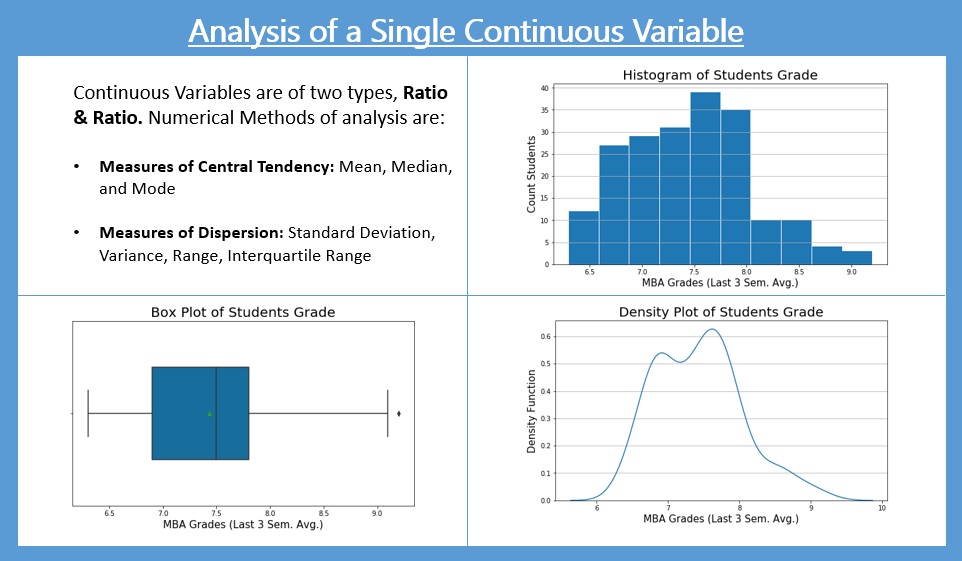
Histograms are a great way of analyzing a single continuous variable. The histogram is an approximate representation of the distribution of numerical data. It is created by converting a continuous variable into categorical by binning/bucketing, i.e. dividing the range of values in the variables into intervals, called class-intervals. The histogram plot is made by having the X-axis represent the class-intervals and the Y-axis represent the class-interval frequencies. The other ways of visually presenting a single continuous variable are Density Plot and Box Plot.

Mean is the most used measure to summarize a single continuous value. The other summary statistics often used are Median, Standard Deviation, Range, Min, Max, Interquartile Range. 

Analysis of the MBA Grades 

Let’s analyze the mba_grades of the students. The field “mba_grades” in the “MBA Students” data is a Continuous Variable

Data Import

# Import the required packages
import pandas as pd
import os
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

# set directory as per your file folder path
os.chdir("d:/k2analytics/datafile")


# read the file
mba_df = pd.read_csv("MBA_Students_Data.csv")

#Set directory as per your folder file path
setwd("D:/k2analytics/datafile")
getwd()

#Read the File

mba_df = read.csv("MBA_Students_Data.csv", header = TRUE)

Numerical Methods to summarize a Single Continous Variable

Let’s write some code to get the Mean, Median, Min, Max, and Standard Deviation measures.

grades_mean = round(mba_df["mba_grades"].mean(),1)
grades_median = round(mba_df["mba_grades"].median(),1)
grades_min = round(mba_df["mba_grades"].min(),1)
grades_max = round(mba_df["mba_grades"].max(),1)
grades_std = round(np.std(mba_df["mba_grades"]),1)

print("Mean grade of the students is :" , grades_mean)
print("Median grade of the students is :" , grades_median)
print("Min grade of the students is :" , grades_min)
print("Max grade of the students is :" , grades_max)
print("Std. Dev of the students grade is :" , grades_std)

Mean grade of the students is : 7.4
Median grade of the students is : 7.5
Min grade of the students is : 6.3
Max grade of the students is : 9.2
Std. Dev of the students grade is : 0.6

#Summary statisitcs 
missing_count = round(is.na(mba_df$avg_grades_of_mba_3_semesters))
grades_mean = round(mean(mba_df$avg_grades_of_mba_3_semesters),2)
grades_median = round(median(mba_df$avg_grades_of_mba_3_semesters),2)
grades_min = round(min(mba_df$avg_grades_of_mba_3_semesters),2)
grades_max = round(max(mba_df$avg_grades_of_mba_3_semesters),2)
grades_std = round(sd(mba_df$avg_grades_of_mba_3_semesters),2)

#Print the Values
cat("The Number of Missing Observations is", missing_count )
cat("The Mean Grade of the Students is", grades_mean)
cat("The Median Grade of the Students is", grades_median)
cat("The Minimum Grade of the Students is", grades_min)
cat("The Maximum Grade of the Students is", grades_max)
cat("The Standard Deviation of the Grade of the Students is", grades_std)

#Output
The Number of Missing Observations is 0
The Mean Grade of the Students is 7.43
The Median Grade of the Students is 7.5
The Minimum Grade of the Students is 6.3
The Maximum Grade of the Students is 9.2
The Standard Deviation of the Grade of the Students is 0.6

Graphical Methods to analyze a Single Continous Variable

Histogram

plt.figure(figsize=(9,5))
plt.hist(mba_df['mba_grades'], rwidth = 0.98)
# rwidth parameter is relative width. 
# It has been used to get spacing between the bars

plt.title('Histogram of MBA Students Grade', fontsize=20)
plt.xlabel('MBA Grades (Last 3 Sem. Avg.)', fontsize=15)
plt.ylabel('Count Students', fontsize=15)
plt.grid(axis='y', alpha=0.75)

Density Plot

plt.figure(figsize=(9,5))
sns.distplot(mba_df['mba_grades'],            
             hist = True, bins=10, 
             kde=True, color='#1F78B4'
            )
## KDE stands for Kernel Density Estimate

plt.title("Histogram & Density Plot \nof MBA Students Grade", fontsize=20)
plt.xlabel('MBA Grades (Last 3 Sem. Avg.)', fontsize=15)
plt.ylabel('Density Function', fontsize=15)
plt.grid(axis='y')

Box Plot

Box plot helps us quickly find outliers in data.

plt.figure(figsize=(9,5))
sns.boxplot(x='mba_grades',
                 data=mba_df, showmeans=True,
                 width=0.5,
                 palette="colorblind")
plt.xlabel('MBA Grades (Last 3 Sem. Avg.)', fontsize=15)

From the Box Plot below, we can see that there is an outlier value. In this case, the outlier is on higher suggest. The interpretation of the outlier in this example will be, that, there is one student who has performed exceedingly well in comparison to all others.

Tabular Methods: Percentile Distribution

# Get the percentile distribution of the students grade
mba_df['mba_grades'].quantile([0,0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.95,0.99,1])

0.00    6.300
0.01    6.500
0.05    6.500
0.10    6.790
0.25    6.900
0.50    7.500
0.75    7.800
0.90    8.200
0.95    8.600
0.99    9.001
1.00    9.200
Name: mba_grades, dtype: float64

Inferences / Take away

We can make the following inferences by seeing the above Descriptive Statistics output:

• The Mean grade of the students is 7.4 and the Standard Deviation is 0.6
• The Histogram shows that there is not much dispersion in the grades of the students.
• The middle 50% of the students are between grade 6.9 to 7.8
• Top 10% of the students have grade above 8.2

Note: Interquartile range is also called the middle 50%.

Practise Exercise 

Analyze the 12th Standard percentage marks of the MBA Students. This information is provided in the variable “ten_plus_2_pct”.

Next Blog

In the next blog, let’s learn “Analysis of two variables”:

• One Categorical and other a Continuous variable
• Both Categorical
• Both Continuous

<<< previous         |         next blog >>>
<<< statistics blog series home >>>