Multiple Linear Regression is a linear regression model having more than one explanatory variable. In our last blog, we discussed the Simple Linear Regression and R-Squared concept. The Adjusted R-Squared of our linear regression model was 0.409. However, a good model should have Adjusted R Squared 0.8 or more. To improve the model performance, we will have to use more than one explanatory variable, i.e., build a Multiple Linear Regression Model.
Multiple Linear Regression
Import Data
We will use the datafile inc_exp_data.csv to learn multiple linear regression in Python/R. Click here to download the file from the Resources section.
/* Import the File */ import pandas as pd inc_exp = pd.read_csv("Inc_Exp_Data.csv") ### R code to import the File ### inc_exp <- read.csv("Inc_Exp_Data.csv")
View Data
inc_exp.head(16) ### Python syntax to view data View(inc_exp)### R syntax to view data

Metadata
| Sr. No. | Column Name | Description |
| 1. | Mthly_HH_Income | Monthly Household Income |
| 2. | Mthly_HH_Expense | Monthly Household Expense (Dependent Variable) |
| 3. | No_of_Fly_Members | Number of Family Members |
| 4. | Emi_or_Rent_Amt | Monthly EMI or Rent Amount |
| 5. | Annual_HH_Income | Annual Household Income |
| 6. | Highest_Qualified_Member | Education Level of the Highest Qualified Member in the household |
| 7. | No_of_Earning_Members | Number of Earning Members |
Hypothesis
A hypothesis is an opinion of what you expect. While framing a hypothesis, remember it should contain an independent and dependent variable. It plays a very important role in machine learning, as such, a Data Scientist should give considerate time to hypothesis development and hypothesis testing.
Herein, I am writing my hypothesis for the first 3 independent variables:
| Independent Variable | Description |
| Mthly_HH_Income | Household having higher monthly income are likely to have relatively higher monthly expense (positive correlation) |
| No_of_Fly_Members | Families having more members are likely to have higher monthly expense (positive correlation) |
| Emi_or_Rent_Amt | The EMI or Rent adds to the monthly cash outflow, as such, they may have higher overall monthly expenses as compared to households having owned residence. |
The hypothesis can be validated using graphical methods like scatter plot, numerical methods like correlation analysis and regression. We will test our hypothesis using:
- Scatter plots (pair plots)
- P-value of the independent variables in the Linear Regression model
Pair Plots
It is a good practice to perform univariate and bivariate analyses of the data before building the models. Pair Plots are a really simple (one-line-of-code simple!) way to visualize relationships between each variable.
Inferences from Pair Plots:
1. The trends between the dependent and independent variables are as per our hypothesis.
2. The distribution of the Mthly_HH_Expense, Mthly_HH_Income, and No_of_Fly_Members variables is some-what Normal Distribution.
3. The Emi_or_Rent_Amt is highly skewed. Many observations have value as 0.
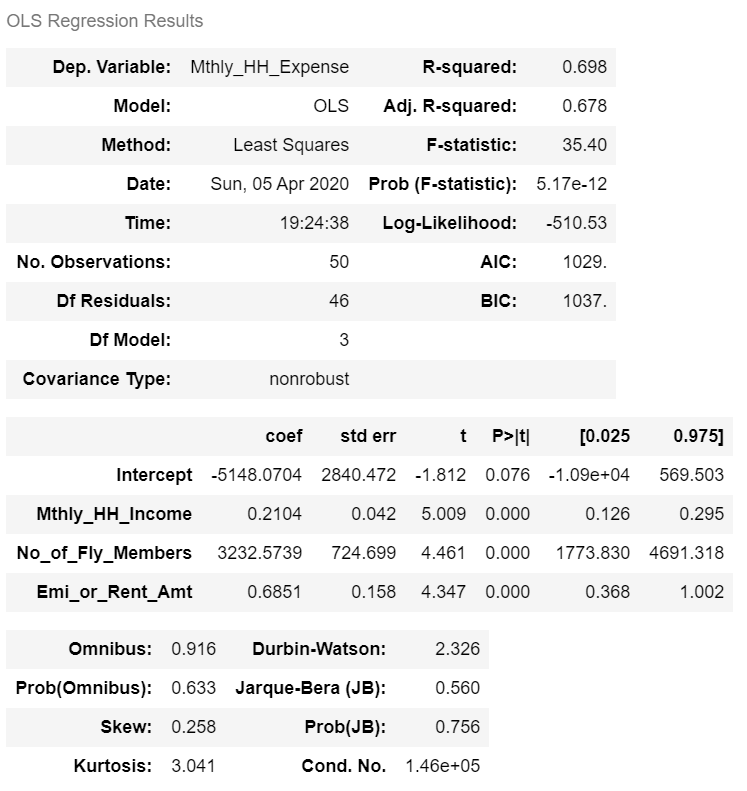
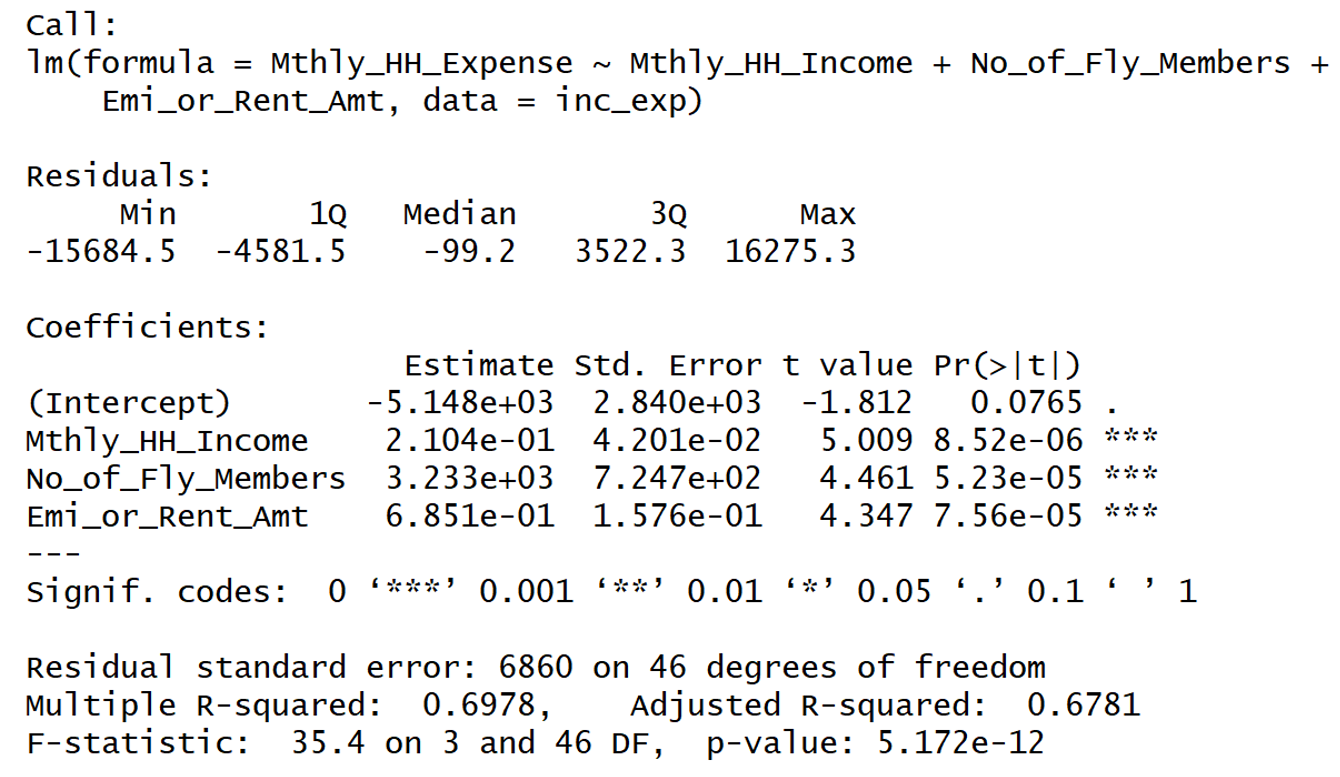
Build the Model
Interpretation of Regression Summary:
1. Adjusted R-squared of the model is 0.6781. This statistic has to be read as “67.81% of the variance in the dependent variable is explained by the model”.
2. All the explanatory variables are statistically significant. (p-values < alpha; assume alpha = 0.0001).
3. The beta coefficient sign (+ or -) are in sync with the correlation trends observed between the dependent and the independent variables.
4. The p-value of the F Test statistic is 5.7e-12. We conclude that our linear regression model fits the data better than the model with no independent variables.
Adjusted R-squared
Adjusted R Squared as the term suggests is R Squared with some adjustment factor. The Adjusted R Squared is a modified version of R Squared that has been adjusted for the number of predictor variables in the model.
Why use Adjusted R-Squared and not R-Squared?
Assume, you have a random variable having a casual relationship with the dependent variable. The addition of such a random variable to the model will still improve the model’s R-squared statistic. However, the Adjusted R Squared statistic will decrease and penalize the model if the explanatory variable does not contribute to the model. It is evident from the Adjusted R-Squared formula.

Where n is No. of Records and k is No. of Variables.
The denominator (n – k – 1) penalizes the R² for every additional variable. If the added variable does not improve the Model R², then the Adjusted R² value will decrease. The drop in Adjusted R² suggests the added term should be dropped from the model.
Let us understand Adjusted R-Squared with practical example
Let us add a Sr_No column to the data and use it as an explanatory variable.
Interpretation
By adding Sr_No term, the R-Squared has increased from 0.6978 to 0.7022. However, Adjusted R-Squared has decreased from 0.6781 to 0.6757. As Adjusted R-Squared has decreased, the added term (Sr_No) should be dropped from the model.
Next Blog
In our upcoming blog, we will explain the concept of Multicollinearity, Prediction using the model, and more.
<<< previous blog | next blog >>>
Linear Regression blog series home




Recent Comments